האם אלוהים יאפשר לילדים לחלות בסרטן? אולי...
ניסיתי להבין את התשובה של קארמה-קון לבעיית המתמטיקה בגמר הבחינות.
חיפשתי הפניות והסברים לבעיה אך ללא הועיל. עדיין לא הצלחתי להבין את ההסברים הנוראיים לבעיה, והתשובה מניחה שאתה יודע שתהליך החשיבה שלהם הוא, מה שאני לא.
יש לזה תרגום לאנגלית לבעיה:
young-il-long-kiyoshi.tumblr.com/post/125623681248/on-the-topic-of-the-final-maths-question-in-the
קישור נוסף שמצאתי מזכיר את הבעיה אך לא מסביר אותה.
angryanimebitches.com/2016/03/assassination-clroomroom-season-2-episode-12-the-principal-is-a-sore-loser/
זה גם סרטון יוטיוב שמסביר את התשובה של קארמה-קון אבל אפילו את ההסבר שלו אני עדיין לא מצליח להבין איך הוא הגיע למסקנה ששטח האטום המרכזי שווה לחצי שטח הקוביה מחולק לשניים. a ^ 3/2
קישור לסרטון: גיאומטריה מוזרה (כיתת רצח S2 E12)
הסיבה שאני מפרסם את זה היא שאין דרך אחרת להבין את הבעיה בלי לשאול בשרשור.
אני רק רוצה להסביר את התשובה ברמת נקודת מבט "תיכונית", ולא דרגת דוקטורט מקצועית ...
אני לא רוצה לשמוע "מרחק שווה", "אינפיניטימלי", "קודקוד" או כל מונח טכני אחר שאיני יכול להבין.
אני יודע שאני דורש יותר מדי, אבל אנא עזור לי להבין איך קארמה-קון הגיע a ^ 3/2. נקודת המבט היחידה שקיבלתי מקארמה היא שכל 8 האטומים יוצרים קובייה משלהם, והנקודה האמצעית של אותה קוביה דמיונית שקולה לכל האטומים שבתוך 8 הקוביות האישיות.
והסרטון אומר גם כן, אבל איך זה עבר בעולם 1/8 ל 2 א? ואז a ^ 3/2
כפי שמוצג כאן:
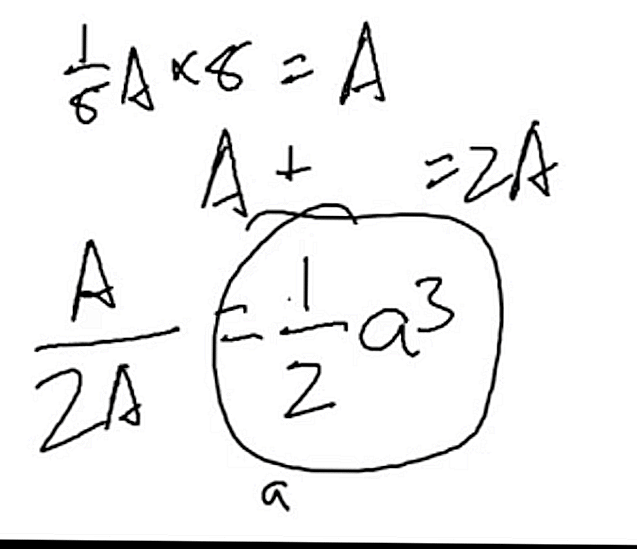
- לשיטת הפיתרון של אסאנו-קון, אני חושב? math.stackexchange.com/questions/3193480/…
כל האטומים בסריג הקריסטל זהים. נניח שנפח האטום בקודקוד (לא בפינה, אם זו פינה תצטרך חשיבה שונה במקצת) הוא B. כל אטום בקודקוד תופס (1/8) B של הקוביה. ראה תרשים.
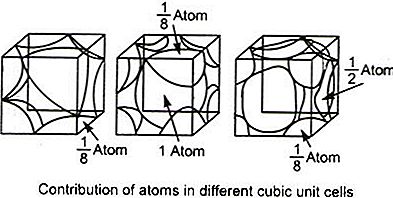
לקוביה באורך a, היא מורכבת מהאטום המרכזי A עם נפח D ו -8 אטומים בקודקודים שכל אחד מהם תופס (1/8) B של הקוביה. לכן,
א3 = D + 8 × (1/8) B
עם זאת, מכיוון שאנו יודעים שהאטומים בקודקודים זהים למעשה לאטום המרכזי, נפח B שווה ל- D ומכאן,
א3 = B + 8 × (1/8) B ==> B = (1/2) א3
QED
כל המונחים הטכניים שציינת הם מה שלמדתי בתיכון שלי. שאלה זו אינה קשה, כפי שאמר קארמה. זו שאלה משולבת של מתמטיקה וכימיה.
7- 1 אבל אני חושב שאתה צריך לשאול את זה בפורום מתמטיקה ולא כאן. זה נראה מביך.
- אבל למה זה מעל 2 בנוסחה a ^ 3/2 ??
- מעל 2 כאן רק אומר לך שלגבי קוביה, רק מחצית מהנפח יהיה הנפח שנלקח על ידי אטום מסוים, ואת שאר הנפח יש לשתף אטומים אחרים.
- אז אם אני עוקב אחריך נכון, A / 8 * 8 = A, וכי שמונת הקודקודים הם תופסים 2 אטומים, כלומר 2 א. ואז מאז א הוא חצי מהקוביה, אז אנחנו כן A / 2A... וכדי לחשב את נפח האטום אנו מכפילים את x, y, z שהוא תלת מימד ובסופו של דבר נוסחתנו למצוא את שטח הקוביה a ^ 3 ימין? ואז אנחנו חצי מזה כך מעל 2? a ^ 3/2
- לא, שמונת האטומים בקודקודים תופסים מקום של אטום אחד בקוביה. A / 2A משמש לאיתור היחס בין הנפח שנלקח מהאטום המרכזי לנפח הכולל הכולל האטום המרכזי והאטומים בקודקודים. אז, מכאן אנו יודעים כי אטום A תופס 1/2 מנפח הקוביה וכך ^ 3/2.
אני יודע שאיחרתי את השאלה הזו, אבל הנה הסבר אולי פשוט יותר. בדיוק הגעתי לבעיה הזו באנימה ורציתי לפתור אותה לפני שהם חושפים את התשובה.
בסדר. יש לך קוביה עם אטום באמצע. מה שתרצה לעשות זה לשבור את הקוביה לשמונה חלקים. קח אחת מהחתיכות האלה. ישנם שני אטומים בפינות מנוגדות (קודקודים). אחד האטומים הללו הוא האטום המרכזי [A] 0 והשני האטום בקצה. ההיגיון הפשוט הולך כי בדיוק מחצית השמינית הזו של קוביה קרובה יותר לאטום אחד מאשר לשני. זה נכון לגבי כל 8 החלקים האחרים, כך שנפח הקוביה קרוב יותר לאטום המרכזי הוא פשוט מחצית מהנפח הכולל.
הבעיה הרבה יותר פשוטה ממה שהיא נראית ואני מודה שחישבתי את הנפח לפי חלקים גיאומטריים לפני שהבנתי שאני טיפש. זה לא דורש הרבה מאוד מתמטיקה. רק אחיזה מוצקה של היגיון וקצת פיקחות.
כביכול, התשובה עצמה במנגה אפילו לא נכונה. אם האטומים תופסים את אותה כמות שטח בתוך כל קובייה, אז הם יהיו מחצית (א) - הקווים הבלתי נראים). למעשה תוכל לחבר אותו לנוסחה לפתרון נפח של כדור שהוא ארבע יותר משלוש פעמים פי פעמים r בהספק 3. במקרה זה, ה- r (רדיוס) שלך הוא a / 2 (מכיוון שהאטומים תופסים אותו כמות שטח, ולכן אטום אחד יתפוס מחצית מהקו הבלתי נראה)
בעיקרון, היית עושה V = 4/3 * π * (a / 2) ^ 3
V = 4/3 * π * a ^ 3/8
V = 4 (ב- 4/3) מבטל את ה- 8 (ב- a ^ 3/8) כך שתקבל 1/3 * π * a ^ 3/2
V = π * a ^ 3/6
שונות: * = פעמים, ^ = בכוח, π = pi.